項目研究和實驗的目的、內容和要解決的主要問題
1. 項目研究目的:
如何利用先進的交通管理系統ATMS、先進的交通信息服務系統ATIS,改進快速路交通運行條件,提升通行效率,是當前許多特大、大型城市面臨的重要課題。優秀的ATMS和ATIS系統必須依賴于準確、實時的交通狀態檢測、估計和預測,因此,針對我國城市快速路典型的道路、交通流特征,充分利用現有的交通流檢測手段,運用合理的數據挖掘處理技術,準確快速估計、預測快速路的交通流狀態,對于改進快速路交通運營管理十分重要。
本課題結合藍牙數據,GPS浮動車數據,以及斷面固定式檢測數據(微波檢測儀),綜合交通流理論的基本原理和快速路交通運行的實際特點, 采用數據融合技術,深入研究城市快速路的交通態勢檢測和評估的多個關鍵理論與方法,最終實現對交通流狀態的估計、對交通發展趨勢的預測、以及對交通事故的檢測。
與單源數據相比,多傳感器數據進行融合可得到統計上的優勢,使用多傳感器數據還可以提高精度。
(l)采用數據融合技術可以獲得更全面的交通流的特征信息
數據融合后,可以獲得任何單一交通流信息采集方法不能獲得的其它的交通流特征信息,增加了交通流特征信息、的維度。
(2)采用數據融合技術可以獲得更加精確的交通流信息
采用單一交通信息采集方法得來的數據質量容易受到采集設備,天氣等客觀
因素的影響,而采用多種交通流信息采集方法可以在一定程度上克服客觀因素的
影響。
(3)采用數據融合技術可以獲得更加準確的交通運行狀態評價結果
融合技術使各單一的交通流信息采集方法相互之間取長補短,因此融合后的數據比單一方法流采集的數據更準確。
基于此,本課題的研究構思如下:
(1)對現有相關研究成果的總結分析基礎上,分析其不足,總結經驗。
(2)采集數據,對數據源進行客觀分析,包括各源數據采集方法及具體數據信息的介紹。
(3)對采集到的數據進行融合,研究最實用的融合算法,
(4)對經過融合處理的評價結果和未經融合處理的評價結果以及由前端融
合和后端融合處理得到的兩個結果進行比較分析,給出結論和建議。
(5)采用計算機編程對程序的設計進行實現。
(5)通過得到的融合數據對交通事故進行檢測。
2.研究內容:
利用卡爾曼濾波進行多源數據融合,進而估計城市快速路的交通狀態,同時對比基于多源數據融合和基于單一數據估計的結果精度。
2.1 基于LWR模型的快速路交通流的刻畫
將路段劃分為I個元胞(每個長度為 ,記作i),時間劃分成H個時間步(每個時長為 ,記作i),時間劃分成H個時間步(每個時長為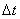 ,記作h)。為了滿足Courant-Friedrichs-Lewy(CFL)穩定性條件,沒有車輛可以在一個時間步中行駛出一個元胞,即 ,記作h)。為了滿足Courant-Friedrichs-Lewy(CFL)穩定性條件,沒有車輛可以在一個時間步中行駛出一個元胞,即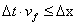 。 。
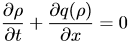 (1) (1)
初始條件:
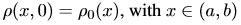 (2) (2)
邊界條件:
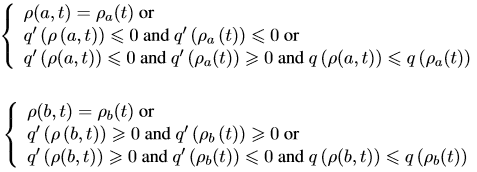 (3) (3)
—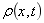 :t時刻,x處密度。 :t時刻,x處密度。
2.2 基于卡爾曼濾波算法的交通流狀態估計
卡爾曼濾波利用遞歸方法解決隨機線性離散系統的狀態或參數估計問題。由狀態方程和觀測方程組成,并利用狀態方程的遞推性,按線性無偏最小均方誤差估計準則,對狀態變量作最佳估計。
(1)狀態方程
如果只考慮整個路段處于自由流動或擁擠狀態,狀態方程如下:
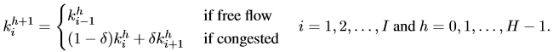 (4) (4)
—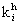 是時間步h的元胞i的密度。 是時間步h的元胞i的密度。
其中δ= w /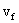 ,w是后向沖擊波速度。 方程(4)假設每個元胞長度相等和同樣的基本圖,在路段中沒有車輛的駛入駛出(即沒有匝道)。 ,w是后向沖擊波速度。 方程(4)假設每個元胞長度相等和同樣的基本圖,在路段中沒有車輛的駛入駛出(即沒有匝道)。
狀態方程矩陣形式如下:
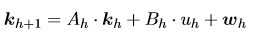
(5)
向量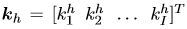 是在時間步h的狀態向量,矩陣Ah和Bh是時變的,它們在時間步h處取決于模式m。在自由流模式中m = 1,在擁塞模式中m = 2。wh表示狀態方程的誤差(由于錯誤或遺漏的計數引起,例如車輛變道)。輸入uh是標量,并且與在計算域的邊界處獲得的測量相關(用于分別計算自由流或擁塞模式下的第一或最后一個元胞的密度)。事實上,如果整個路段在自由流或擁擠模式下: 是在時間步h的狀態向量,矩陣Ah和Bh是時變的,它們在時間步h處取決于模式m。在自由流模式中m = 1,在擁塞模式中m = 2。wh表示狀態方程的誤差(由于錯誤或遺漏的計數引起,例如車輛變道)。輸入uh是標量,并且與在計算域的邊界處獲得的測量相關(用于分別計算自由流或擁塞模式下的第一或最后一個元胞的密度)。事實上,如果整個路段在自由流或擁擠模式下:
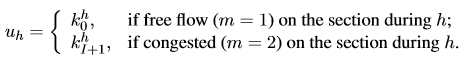
(6)
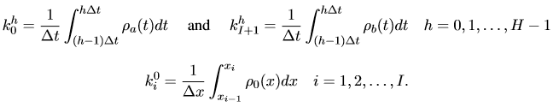
(7)
其中 、 、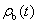 為邊界條件; 為邊界條件;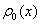 是初始條件。 是初始條件。
(2)觀測方程
觀測方程如下:

(8)
yh是觀測矢量,vh是測量誤差。卡爾曼濾波還假設wh和vh是獨立的,且服從均值為的正態分布。Ch的大小取決于h時間步處的拉格朗日觀測值來自哪里,并且它僅包含0和1(假定可以從拉格朗日傳感器觀測到局部密度)。拉格朗日觀測來自不同的元胞,并且在連續時間步長之間的觀測數量可能不同。因此,等式(8)中的觀測矢量y h將在不同的時間步長具有不同的維度。后者意味著矩陣Ch也將在每個時間步長具有不同的維度。
(3)遞歸方程
卡爾曼濾波遞歸方程如下:
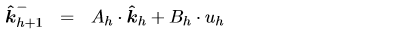 (9) (9)
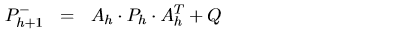 (10) (10)
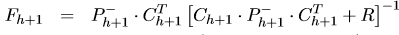 (11) (11)
 (12) (12)
 (13) (13)
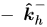 :kh的先驗狀態估計; :kh的先驗狀態估計;
 :kh的后驗狀態估計; :kh的后驗狀態估計;
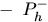 :先驗估計誤差協方差矩陣; :先驗估計誤差協方差矩陣;
 :后驗估計誤差協方差矩陣。 :后驗估計誤差協方差矩陣。
假定已知初始條件 和 和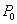 。 Q和R分別是過程協方差矩陣和測量誤差協方差矩陣。 Fh是時間步h的卡爾曼增益。矩陣Ch在每個時間步長具有不同的維度,這意味著協方差矩陣R的維數可變。 。 Q和R分別是過程協方差矩陣和測量誤差協方差矩陣。 Fh是時間步h的卡爾曼增益。矩陣Ch在每個時間步長具有不同的維度,這意味著協方差矩陣R的維數可變。
在每個時間步開始時,交通狀態需要被識別(為了決定矩陣A和B)。一旦在時間步h + 1的開始已經識別出模式,則使用公式(9)和(10)來分別獲得先驗密度估計和協方差(使用從檢測器站提供的歐拉數據)。此時拉格朗日數據將提供給模型,即一些元胞在時間步h + 1處的觀測密度是已知的(在時間步h + 1的拉格朗日傳感器的數量和位置將決定觀測密度的數量和哪些元胞的密度被觀測)。利用該信息,可以構造觀測矢量 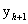 和矩陣 和矩陣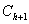 。然后,使用公式(11)計算卡爾曼濾波器增益。最后,利用式(12)和(13)分別得到后驗密度估計和后驗估計協方差矩陣。若在h+1沒有觀測數據,矩陣 。然后,使用公式(11)計算卡爾曼濾波器增益。最后,利用式(12)和(13)分別得到后驗密度估計和后驗估計協方差矩陣。若在h+1沒有觀測數據,矩陣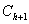 等于0,意味著卡爾曼增益也是0,因此后驗密度估計等于先驗密度估計。 等于0,意味著卡爾曼增益也是0,因此后驗密度估計等于先驗密度估計。
3. 擬解決的主要問題:
(1)交通流狀態數據的采集
(2)數據處理及融合方法
(3)基于卡爾曼濾波的快速路交通狀態估計
(4)基于交通流數據的交通事故發生預測
(5)設計程序的實現
|